Longest Side Of Right Triangle

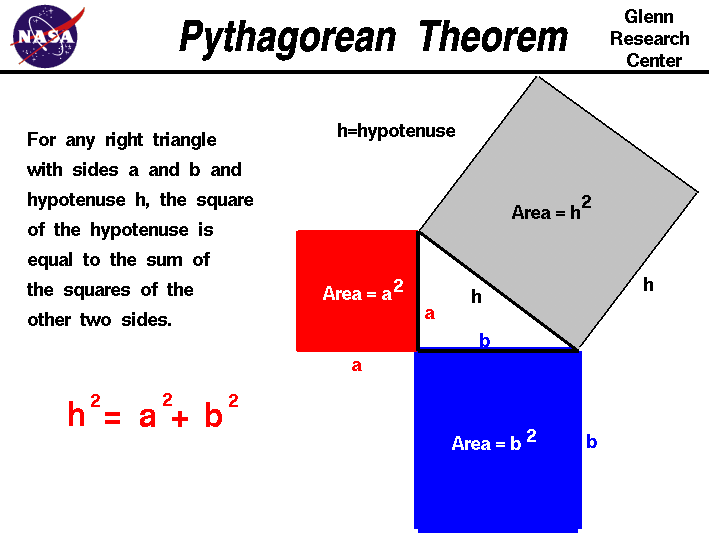
Computer drawing of a right triangle giving the Pythagorean Theorem that relates the length of the sides.

To amend sympathize certain problems involving shipping and propulsion information technology is necessary to use some mathematical ideas from trigonometry the study of triangles. Let u.s. begin with some definitions and terminology which nosotros volition use on this slide. We start with a right triangle. A right triangle is a iii sided figure with one angle equal to xc degrees. A 90 degree bending is chosen a correct angle and that is where the right triangle gets its name. We define the side of the triangle opposite from the right angle to be the hypotenuse, h. Information technology is the longest side of the three sides of the right triangle. The word "hypotenuse" comes from two Greek words meaning "to stretch", since this is the longest side. We are going to label the other two sides a and b. The Pythagorean Theorem is a argument relating the lengths of the sides of whatever correct triangle.

The theorem states that:

For whatsoever correct triangle, the square of the hypotenuse
is equal to the sum of the squares of the other two sides.

Mathematically, this is written:

h^two = a^two + b^two

The theorem has been known in many cultures, by many names, for many years. Pythagoras, for whom the theorem is named, lived in ancient Hellenic republic, 2500 years ago. It is believed that he learned the theorem during his studies in Egypt. The Egyptians probably knew of the relationship for a thousand years before Pythagoras. The Egyptians knew of this relationship for a triangle with sides in the ratio of "3 - four - 5".

5^2 = iii^2 + four^2

25 = ix + 16

Pythagoras generalized the event to whatsoever right triangle. There are many unlike algebraic and geometric proofs of the theorem. Most of these begin with a construction of squares on a sketch of a basic correct triangle. On the figure at the pinnacle of this page, we show squares drawn on the three sides of the triangle. A square is the special example of a rectangle in which all the sides are equal in length. The expanse A of a rectangle is the product of the sides. So for a square with a side equal to a, the area is given by:

A = a * a = a^2

So the Pythagorean theorem states the surface area h^two of the square fatigued on the hypotenuse is equal to the surface area a^2 of the square fatigued on side a plus the area b^ii of the square drawn on side b.

Here'south an interactive Coffee program that permit's you see that this area relationship is true:

We begin with a right triangle on which nosotros have constructed squares on the two sides, one blood-red and one blue. We are going to break upward the pieces of these two squares and move them into the greyness foursquare expanse on the hypotenuse. We won't loose whatsoever cloth during the performance. And so if we tin exactly fill upward the square on the hypotenuse, we accept shown that the areas are equal. You work through the construction past clicking on the push labeled "Next". Yous can become "Back" and repeat a section, or go all the way dorsum tothe beginning by clicking on "Reset".

What is information technology doing? The beginning pace rotates the triangle down onto the blue square. This cuts the blueish square into three pieces, two triangles and a red rectangle. The two triangles are exactly the same size as the original triangle. The "bottom" of the original triangle exactly fits the vertical side of the square, because the sides of a square are equal. The cherry rectangle has its vertical sides equal to the base of the original triangle, and its horizontal sides equal to the difference betwixt the "bottom" side and the "vertical" side of the original triangle. Using the terminology from the figure at the summit of this page, the dimensions of the red rectangle are:

vertical length = b

horizontal length = b - a

The side by side footstep is to movement the ruby rectangle over adjacent to the red square. The rectangle sticks out the top of the carmine square and the two triangles remain in the blue square. The next footstep is to motility one of the blueish triangles vertically into the hypotenuse foursquare. Information technology fits exactly forth the side of the hypotenuse square because the sides of a square are equal. The next step is to move the other blue triangle into the hypotenuse square. (We are one-half way there!) The next stride is to slide the form of the original triangle to the left into the red region. The triangle cuts the reddish region into three pieces, two triangles and a pocket-size yellow square. The original triangle fits exactly into this region because of two reasons; the vertical sides are identical, and the horizontal side of the red region is equal to the length of the red square plus the horizontal length of the red rectangle which we moved. The horizontal length of the red region is:

horizontal length = a + (b - a) = b

The horizontal length of the red region is exactly the length of the horizontal side of the original triangle. The xanthous square has dimensions b - a on each side. The side by side step is to movement one of the red triangles into the hypotenuse square. Over again it's a perfect fit. The side by side stride is to move the concluding red triangle into the hypotenuse square. At present if we look at the grey square that remains in the hypotenuse foursquare, we see that its dimensions are b - a; the long side of the triangle minus the brusk side. The final step is to movement the yellowish square into this hole. It's a perfect fit and we have used all the material from the original red and blue squares.

Activities:

Guided Tours

Navigation ..